함수
하나의 특별한 목적의 작업을 수행하기 위해 독립적으로 설계된 코드들의 모임으로 하나의 단위 의미

재귀(recursion)
자신을 재 참조하는 방법
- 순환 또는 재귀적 : 어떤 사건이 자기 자신을 포함하고 다시 자기 자신을 사용해 정의되는 것
- 예) 버스 기다리기(x)
- 버스를 기다린다.
- 버스가 오면 버스 번호를 확인
- 만일 버스 번호가 x면 버스를 타고 버스 기다리기(x) 종료
- 버스 번호가 x가 아니면 버스 기다리기(x) 다시 수행
재귀 함수(recursion function)
자신을 반복적으로 호출해 수행하는 방식을 통해 주어진 문제를 해결하는 함수
유형
- 직접 순환 : 자신을 직접 호출
- 간접 순환 : 피호출 함수 내에서 호출 함수를 다시 호출

재귀 예시
1에서 n까지 자연수 더하기

1부터 입력된 수까지의 합을 구하기
#include <stdio.h>
int sum(int n);
int main(){
int n;
printf("입력 값=");
scanf("%d", &n);
printf("1부터 %d까지의 합은 %d이다.", n, sum(n));
}
int sum(int n) {
if(n==1 ) //종료조건
return 1;
else return n+sum(n-1);
}
result
입력 값=8
1부터 8까지의 합은 36이다.
계승
Factorial(n)에 대한 재귀함수
- n! = n*n(-1)! n >= 1
- 1 n = 0

1부터 입력된 수까지의 factorial 값을 구하기
#include <stdio.h>
int factorial(int n){
if (n == 1) //n이 1일 때, 1을 반환하고 재귀호출을 끝냄
return 1;
return n * factorial(n - 1);//n과 factorial 함수에 n - 1을 넣어서
//반환된 값을 곱함
}
int main(){
int n;
printf("입력 값= ");
scanf("%d", &n);
printf("입력값 %d의 factroial=%d이다.", n, factorial(n));
return 0;
}
result
입력 값= 5
입력값 5의 factroial=120이다.
피보나치 수열
- f0 = 0 if n = 0
- f1 = 1 if n = 1
- fn = fn-1 + fn-2 otherwise
- 피보나치 수열 : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34
- 피보나치 수열의 항은 재귀적으로 다시 다른 두개(fn-1 + fn-2)의 피보나치 항으로 정의됨
int fibonacci(int n) {
if(n == 0 || n == 1) // F(0) = 0 and F(1) = 1, 종료조건
return n;
else
// F(n) = F(n-1 ) + F(n-2), 재귀 함수에서 재귀되는 부분
return fibonacci(n-1) + fibonacci(n-2);
}1부터 입력된 수까지의 피보나치 수열을 구하기
#include <stdio.h>
int main(){
int i, n, t1 = 0, t2 = 1, nextTerm;
printf(“피보나치 수 입력 : ");
scanf("%d", &n);
printf("피보나치 수열 : ");
for (i = 1; i <= n; ++i) {
printf("%d, ", t1);
nextTerm = t1 + t2;
t1 = t2;
t2 = nextTerm;
}
return 0;
}
피보나치 수 입력 : 5
피보나치 수열 : 0, 1, 1, 2, 3#include <stdio.h>
int fib(int n){
if (n <= 1) return n;
return fib(n-1 ) + fib(n-2 );
}
int main (){
int n;
printf("피보나치 수 입력 : ");
scanf("%d", &n);
printf("입력된 수%d의 피보나치 수열의 합: %d", n, fib(n));
return 0;
}
result
피보나치 수 입력 : 7
입력된 수7의 피보나치 수열의 합: 13
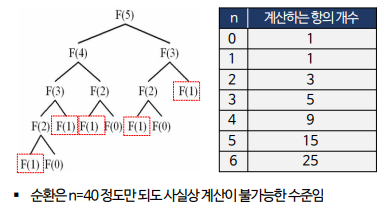
재귀의 함정
- Function Call이 쓸데 없이 겹쳐지게 됨
- 시간복잡도 - O(2^n), 높이 n인 이진 트리의 총 노드 수는 2^n - 1
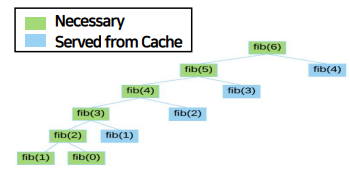
Memoization 기법
- 프로그램이 동일한 계산을 반복해야 할 때 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거해 프로그램 실행속도를 빠르게 하는 기술. 함수를 위한 캐싱 기법이 있음
- 주어진 입력에 대해 항상 동일한 출력을 반환하는 알고리즘에 한해 사용
- Memoization을 사용하면 2000까지 정도는 계산 가능
- 시간복잡도 - O(n)
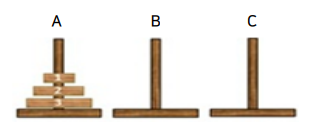
하노이의 탑
- 여러 개의 원반과 세 개의 기둥이 있는데 원반의 크기는 각각 다름
- 먼저 모든 원반은 기둥 A (source)에 위치하지만 그 원반들을 기둥 C(destination)로 이동해야함
- 한번에 한개 원반만 옮길 수 있고 어떤 경우에도 원반은 그 보다 작은 원반위에 올려질 수 없음
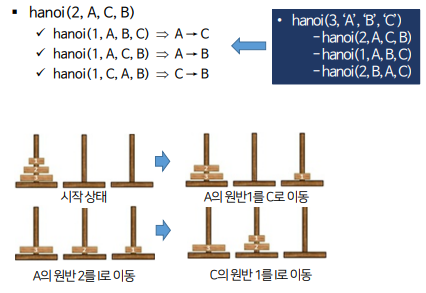
재귀 알고리즘으로 해결
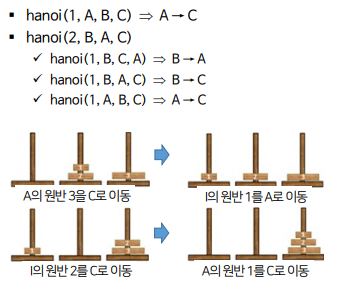
모든 원반을 처음 시작한 기둥 A에서 다른 하나의 중간 기둥B를 사용해 n개의 원반을 목적기둥 C로 이동할 때
- 가장 큰 원반을 제외한 나머지 개의 원반을 A에서 B로 이동
- A에 남아있던 한 개의 원반을 C로 이동
- 작은 피라미드를 B에서 A로 이동
- 1단계와 2단계에서 했던 과정을 반복해서 수행, 이때 3단계 원반의 개수는 1단계 보다 1개 적어짐
void hanoi(int n, int from, int aux, int to) {
if (n == 1) move(from, to); //종결조건
else {
hanoi(n - 1, from, to, aux);
hanoi(1, from, aux, to); // move(from, to);
hanoi(n - 1, aux, from, to); }
}
#include <stdio.h>
void towerOfHanoi(int n, char from, char aux, char to){
if (n == 1){
printf("\n Move disk 1 from %c to %c", from, to);
return;
}
towerOfHanoi(n-1, from, to, aux);
printf("\n Move disk %d from %c to %c", n, from, to);
towerOfHanoi(n-1, aux, from, to);
}
int main(){
int n = 3; // Number of disks
towerOfHanoi(n, 'A', 'B', 'C');
return 0;
}
result
Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 3 from A to C
Move disk 1 from B to A
Move disk 2 from B to C
Move disk 1 from A to C
재귀 알고리즘을 비재귀 알고리즘으로 변환
변환 과정
재귀 구조(함수)는 반복 구조로, 반복 구조를 사용하는 알고리즘은 재귀 구조를 통해 구현하는 것이 가능
재귀 함수의 메모리와 성능에 대한 문제점을 해결할 수 있음
- 재귀 함수에서 비재귀를 위한 초기조건을 구함
- 재귀 함수의 현재 값과 다음 값과의 관계를 이용해 다음 값을 구하는 관계식을 유도
- 관계식을 비 재귀로 표현

재귀 함수의 특징 및 고려사항
재귀 함수의 특징
- 어떤 문제를 해결하기 위해 함수가 자기 자신을 호출할 때마다 문제가 작아지고 단순해져 문게 해결점에 도달함.
- 프렉탈 모형 - 일부 작은 조각이 전체와 기하학적으로 비슷하게 무한대로 반복하며 만들어내는 형태
- 설명하기 어렵고 복잡한 문제를 간단히 정의할 수 있고 표현법이 매우 간단함(코딩이 단순하고 가독성이 좋으며, 오류수정이 용이하고 변수 사용이 줄어듬
- 호출 시 매번 스택(기억공간) 사용으로 수행시간 오버헤드 및 오버플로우 발생 가능
재귀 함수 고려사항
- 재귀 호출을 끝낼 수 있는 종료조건 확인, 하지 않으면 시스템이 무한 반복으로 메모리 오류 발생
- 재귀 호출로 프로그램이 간단해질 수 있는지에 대한 확인 필요
- 각 재귀 호출은 활성 레코드에 관련된 정보(지역변수, 인수, 반환 주소등)을 스택에 저장해야 하므로 기억 공간이 충분한지 확인 후에 사용해야함
- 재귀 호출 사용해 이점이 없을 경우 비 재귀 방법 사용이 좋음
- 재귀 호출은 문맥 변경이 일어나기 때문에 재귀 호출은 반복 호출에 비해 수행 시간이 더 느림
- 효율적인 프로그램 디자인을 위해서 권장되는 방법은 아님
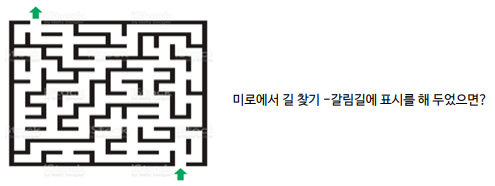
백트래킹
문제를 해결하는 과정에서 고려할 수 있는 모든 경우의 수를 탐색해보는 일반적인 알고리즘 기법
- 탐색 과정에서 해를 찾는 도중 해가 아니면, 되돌아가서 다시 해를 찾는 기법 (한정 조건을 가진 문제(constraint satisfaction problem)
- car navigation system, decision problem, optimization problem, enumeration problem 등에 사용
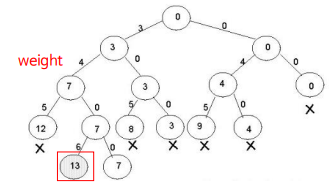
상태공간 트리(state space tree)
- 백트래킹을 위해 고려해야할 모든 경우의 수(상태)를 트리 구조를 이용해 표현한 것
- 해를 찾기 위해 탐색할 필요가 있는 모든 후보들을 포함하는 트리
- 트리의 모든 노드들을 방문하면 해를 찾을 수 있음
- 근노드에서 출발해 체계적으로 모든 노드를 방문하는 절차를 기술
관련 용어
- 노드의 유망성(promising), 특정 제약(constraints) 또는 제한(limitations) 조건 검사
- 문제를 풀면서 여러 조건을 고려한 다양한 상태에 대해 그 상태가 되는 답이 나올때까지 검사하며 점진 탐색
- 해답이 나올 가능성 없는 노드는 유망하지 않음(non-promising), 해당 노드의 서브 트리 탐색은 무의미
- 그렇지 않으면 유망함
- 그래프 탐색 방법- 깊이선탐색(depth first search, DFS)과 너비우선탐색, 최선 우선 탐색
- 가지치기(pruning) - DFS로 모든 정점을 탐색하는 과정에서 조건에 맞지 않는 가지(탐색 경로)를 자르고 다른 탐색 경로로 돌아가 시간을 절약하기 위한 과정
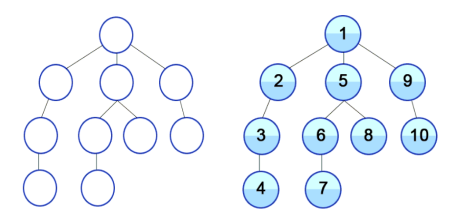
깊이 우선 탐색 방법
- 맹목적 탐색방법의 하나로 시작점부터 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
- 탐색트리에서 근노드(root node)를 선택해 방문하고, 그 노드의 모든 후손 노드(descendant)들을 차례로 (왼쪽에서 오른쪽)방문
- DFS 알고리즘

백트래킹 알고리즘
DFS를 통한 백트래킹 절차
- 상태 공간 트리의 DFS를 실시
- 각 노드가 유망한지 점검
- 노드가 유망하지 않으면, 노드의 부모 노드로 돌아가 탐색
void checknode(node v) {
if (promising(v))
if (there is a solution at v)
write the solution;
else
for (each child u of v) checknode(u);
}
백트래킹과 DFS차이
- DFS 깊이 우선 탐색으로 모든 노드 방문을 목표로함
- 완전 탐색으로 인해 유한 시간 내 끝나지 않을 수도 있음(해가 없는 경로에 깊이 빠질 가능성)
- 해를 구했을 때, 최적이 아닐 수 있음
- 백트래킹 - 불필요한 탐색을 하지 않기 위해, 가지치기를 통해 유망하지 않은 경우의 수 줄이는 것을 목표
- 일단 방문해보고 더 이상 진행이 되지 않으면 돌아옴
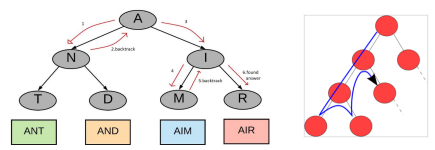
대표적인 백트래킹 문제 : N-queen
- NxN 크기의 체스판에 N개의 queen을 서로 공격할 수 없도록 배치하는 문제
- Queen은 다음과 같이 이동할 수 있으므로 서로 상대방을 위협하지 않기 위해서는 같은 행이나 같은 열, 같은 대각선상에 위치하지 않아야 함
- 무작정(brute force) 방법(4x4 board) - N의 크기가 커질수록 연산량이 기하급수적으로 증가함

N-queen 문제의 이해
- 전제 조건에 따라
- 각 queen을 각각 다른 행에 할당한 후에, 어떤 열에 위치하면 해답은 얻을 수 있는지를 차례대로 점검
- 각 queen은 4개의 열 중에서 한 열에 위치할 수 있기 때문에 해답을 얻기 위해 점검해보아야 하는 모든 경우의 수는 4^4 = 256가지
- 상태공간 트리
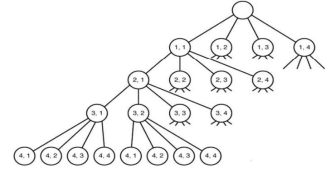
- DFS탐색을 통해 모든 branch를 최대 깊이까지 검색하지 않고, 요구사항에 맞게 해당 노드의 유망성 검사 및 가지치기를 통해 탐색 공간을 줄임
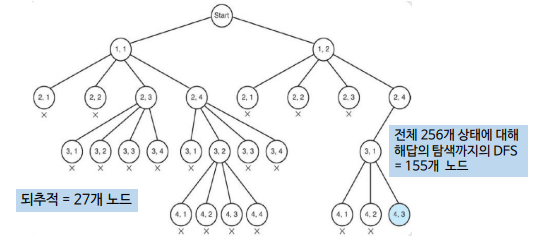
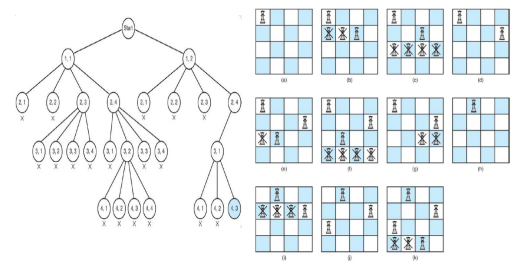
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int chess_board[20], count; //board에 놓여진 queen의 column 위치 값 저장
void nqueen_function(int row, int num){ // queen들의 제한조건 만족 체크
int col;
for(col = 1; col<= num; col++){
if(placeholder(row, col)){//queen이 위치할 곳을 체크하기 위해 함수 호출
chess_board[row] = col;
if(row == num){ //모든 queen들이 board에 위치했는지 검사
display(num); //위치했으면 출력 함수 display()호출
}
else{
nqueen_function(row + 1, num); //남아있는 queen들을 배치하기
//위해 함수 nqueen_function() 호출
}
}
}
}
int display(int num){
int m, n;
printf("\n\n\tPossible Solution %d:\n\n", ++count);
for(m = 1; m <= num; m++){
printf("\t[%d]", m);
}
for(m = 1; m <= num; m++){
printf("\n\n[%d]", m);
for(n = 1; n <= num; n++){
if(chess_board[m] == n){
printf("\tQ"); //(i, j) 위치에 queen(Q)을 출력
}
else{
printf("\t*"); //queen배치가 없는 슬롯에 *을 출력
}
}
}
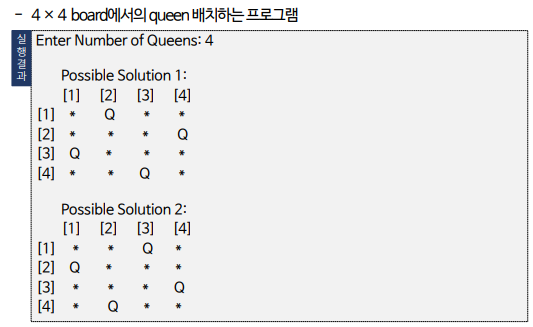
}int main(){
int num;
printf("Enter Number of Queens:\t");
scanf("%d", &num);
if(num <= 3 ){
printf("\nNumber should be greater than 3 to form a Matrix\n");
}
else{
nqueen_function(1, num); //nqueen_function() 호출
}
printf("\n\n");
return 0;
}
학습정리
- 프로그래밍 언어에서 함수는 하나의 특별한 목적의 작업을 수행하기 위해 독립적으로 설계된 코드들의 모임으로 하나의 프로그램 단위
- 재귀함수는 자기 자신을 반복적으로 호출해 수행하는 방식을 통해 주어진 문제를 해결하는 함수
- Memoization 기법은 프로그램이 동일한 계산을 반복해야 할 때 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거해 프로그램 실행속도를 빠르게 하는 기술
- 백트래킹 알고리즘은 문제를 해결하는 과정에서 고려할 수 있는 모든 경우의 수를 모두 탐색해보는 일반적인 알고리즘 기법으로 탐색 과정에서 해를 찾는 도중 해가 아니면, 되돌아가서 다시 해를 찾아가는 기법
반응형
'23년 이전 글 > 자료구조' 카테고리의 다른 글
| 큐, 우선순위 큐, 데크 (0) | 2022.08.06 |
|---|---|
| 스택 자료구조 (0) | 2022.07.26 |
| 구조체와 범용 리스트 (0) | 2022.07.24 |
| 선형 리스트와 배열 (0) | 2022.07.23 |
| 추상 자료형, 알고리즘 (0) | 2022.07.06 |
