순차구조
순차 자료구조(sequential structure)
- 구현할 자료들을 논리적인 순서대로 메모리에 연속하여 저장해 구현하는 방식
- 논리적인 순서와 물리적인 순서가 항상 일치
- 순차 자료구조는 배열을 이용해 구현함
| 구분 | 순차 자료구조 | 연결 자료구조 |
| 메모리 저장방식 | - 메모리의 저장 시작 위치부터 빈자리 없이 자료를 순서 대로 연속하여 저장 - 논리적 순서와 물리적 순서가 일치하는 구현 방식 |
메모리에 저장된 물리적 위치나 물리적 순서와 상관없이 링크에 의해 논리적인 순서를 표현하는 구현 방식 |
| 연산 특징 | - 삽입, 삭제 연산을 해도 빈자리 없이 자료가 순서대로 연속하여 저장 - 변경된 논리적인 순서와 저장된 물리적인 순서가 일치 |
삽입, 삭제 연산을 하여 논리적인 순서가 변경되어도 링크 정보만 변경되고 물리적인 순서는 변경되지 않음 |
| 프로그램 기법 | 배열을 이용한 구현 | 포인터를 이용한 구현 |
선형 리스트(linear list)
- 자료를 구조화하는 가장 기본적인 방법으로 자료를 나열한 목록 또는 자료간 순서를 갖는 리스트
- 순서 -> 원소의 특성에 의한 논리적 순서
- 리스트 -> 원소를 일렬로 정렬해 놓은 것
- 리스트의 자료는 노드 또는 요소라고 함
특징
- 자료들이 순서대로 연속적으로 메모리에 저장됨. 원소들의 논리적 순서와 같은 순서로 기억공간에 저장(순차구조)하고 원소들의 논리적 순서 = 원소가 저장된 물리적 순서
- 삽입, 삭제 시 순서에 변함이 없음
- 접근속도가 빠름
- 알고리즘이 간단함
표현형식
- 선형리스트(선형순차리스트)에서 원소를 나열한 순서는 원소들의 순서가 됨
- 표기 L = (e1,e2...) L 리스트 이름, ei = 자료형이 같은 원소, 공백리스트 L=()

선형 리스트의 저장
원소들이 나열된 논리적 순서와, 메모리 저장된 물리적 순서가 일치하는 자료구조 방식(배열)로 구현

선형 리스트 원소 삽입
원소 삽입
- 선형리스트 중간에 원소가 삽입되면 그 이후 원소들은 한 자리씩 자리를 뒤로 이동해 물리적 순서를 논리적 순서와 일치시켜야함
삽입 방법
- 삽입할 빈자리 만들기
- 삽입할 자리 이후의 원소들을 한 자리씩 뒤로 자리 이동
- 준비한 빈자리에 원소 삽입
삽입할 자리를 만들기 위한 자리 이동 횟수
- n+1 개의 원소로 이루어진 순서리스트에서 k번째 자리에 원소를 삽입하는 경우
- k번째 원소부터 마지막 n번째 원소까지 (n-k+1)개의 원소를 이동
- 이동횟수 = n-k+1 = 마지막 원소의 색인 - 삽입할 자리의 색인 + 1

선형 리스트의 원소 삭제
원소의 삭제
- 선형리스트 중간에 원소가 삭제되면 그 이후 원소들은 한 자리씩 자리를 앞으로 이동해 물리적 순서를 논리적 순서와 일치시킴
삭제 방법
- 원소를 삭제
- 삭제한 빈 자리 채우기 -> 삭제한 자리 이후 원소들을 한자리씩 앞으로 이동
삭제 후 빈자리를 채우기 위한 자리 이동 횟수
- (n+1)개의 원소로 이루어진 순서 리스트에서 k번째 자리의 원소를 삭제한 경우
- (k+1)번째 원소부터 마지막 n번째 원소까지 (n-(k+1)+1)개의 원소를 이동
- 이동횟수 = n-(k+1)+1 = n-k = 마지막 원소의 색인 - 삭제한 자리의 색인

삽입삭제 연산의 특징
- 삭제/삽입 시 후속 원소들을 한 자리씩 전후로 이동
- 일정시간 내 리스트의 원소들에 대한 검색 및 갱신이 가능
- 삽입 시 평균 이동횟수 (m) = n+1/2
- 삭제 시 평균 이동횟수 (m) = n-1/2
- 리스트의 길이가 클 경우 = (삽입, 삭제) ~ n/2
배열
- 동일한 자료형(기본자료형, 구조체, 포인터)들이 <색인, 원소>의 순서쌍으로 집단화한 선형자료구조(순차적 저장, 유한집합)
특징
- 하나의 변수에 여러 값을 저장하는 데 쓰이는 정적 리스트 구조. 원소의 갯수가 정해져서 항상 마지막 원소가 존재함
- 색인(index)를 이용해서 자료형이 같은 데이터를 관리 및 집합 내에서 상대적인 위치의 식별(접근)이 가능함
- 순차적 접근 -> 주소 계산이 쉬움. 임의접근 -> 주소만 있으면 일정 시간 내 접근 가능
- 시스템 데이터형으로 주로 연속 기억공간 할당으로 구현되며 기억공간 할당 방식과는 독립적
- 정보의 은닉 -> 색인을 가지고 어떻게 원소 값에 접근하느냐는 사용자는 몰라도 됨
배열 ADT

배열 연산
- 순회 : 배열의 모든 원소에 대한 인쇄 및 합산
- 반복 구조를 이용
- 실행 시간을 빠르게 하기 위해 프로그래밍 언어의 저장방법에 맞게 작성
- 삽입/삭제 : 각 원소들을 이동해야 하기 때문에 삽입/삭제가 빈번할 경우 배열은 효과적인 자료구조가 아님 -> 연결리스트 구조를 이용
- 정렬 및 탐색
배열의 크기
배열의 요소를 참조하기 위해 행/열에 대한 두개 이상의 색인을 사용
- 1차원 = (상한 - 하한 + 1)
- 2차원 = (상한 - 하한 + 1) * (상한 - 하한 + 1)
- 3차원 = (상한 - 하한 + 1) * (상한 - 하한 + 1) * (상한 - 하한 + 1)
배열을 이용하는 방법 특징
배열의 색인은 배열 원소의 순서를 나타냄
- 물리적 순서로 논리적 순서를 표현
- 리스트 원소 e와 ei+1 -> 배열 색인 i와 i+1에 대응
- 원소 크기가 1이고 시작주소가 b일 때
- 기억장소 이용률 = 정보들의 총수 / 비트들의 총수 = 100%
1차원 배열을 이용한 구현

#include <stdio.h>
#include <stdio.h>
int main(){
int i, sale[4]={160, 245, 139, 450};
for (i=0; i<4; i++){
printf("address of sale[%d]=%d: %u \n", i, sale[i], &(sale[i]));
}
return 0;
}
result
address of sale[0]=160: 6487552
address of sale[1]=245: 6487556
address of sale[2]=139: 6487560
address of sale[3]=450: 6487564
배열에 원소 삽입
#include <stdio.h
>
#define MAX_SIZE 100
int main(){
int arr[MAX_SIZE];
int
i, size, num, pos
;
printf("Enter size of the array : "); //배열의 크기를 입력
scanf("%d", &size);
printf("Enter elements in array : "); //배열에 임의의 원소를 입력
for(
i=0;
i<size;
i++){
scanf("%d", &arr
[
i]);
}
printf("Enter element to insert : "); //삽입할 새로운 원소를 입력
scanf("%d", &num);
printf("Enter the element position : "); //삽입할 위치를 입력
scanf("%d", &pos);if(pos > size+1 || pos <= 0){ //삽입 위치에 대한 조건 검사
printf("Invalid position! Please enter position between 1 to %d", size);
}
else
{
for(i=size;i>=pos;i--) { //오른쪽으로 이동, 삽입할 원소의빈 공간 확보
arr[i] = arr[i-1];
}
arr[pos-1] = num; //새로운 원소를 주어진 위치에 삽입
size++; //size를 하나 증가
printf("Array elements after insertion : "); //삽입후 전체 원소 출력
for(i=0;i<size;i++){
printf("%d\t", arr[i]);
}
}
return 0;
}result
Enter size of the array : 4
Enter elements in array : 10 20 30 40
Enter element to insert : 15
Enter the element position : 2
Array elements after insertion : 10 15 20 30 40배열에서 원소 삭제
#include <stdio.h>
#define MAX_SIZE 100
int main(){
int arr[MAX_SIZE];
int i, size, pos;
printf("Enter size of the array : "); //배열의 크기를 입력
scanf("%d", &size);
printf("Enter elements in array : "); //배열에 임의의 원소를 입력
for(i=0; i<size; i++){
scanf("%d", &arr[i]);
}
printf("Enter the element position to delete : "); //삭제할 원소의 위치를 입력
scanf("%d", &pos);if(pos < 0 || pos > size){ //삭제 위치에 대한 조건 검사
printf("Invalid position! Please enter position between 1 to %d", size);
}
else
{
for(i=pos-1;i<size-1;i++){ //현재 원소 값을 다음 원소 값으로 복사
arr[i] = arr[i + 1];
}
size--; // size를 하나 감소
//삭제후 전체 원소 출력
printf("\nElements of array after delete are : ");
for(i=0;i<size;i++){
printf("%d\t", arr[i]);
}
}
return 0;
}result
Enter size of the array : 5
Enter elements in array : 10 20 30 40 50
Enter the element position to delete : 3
Elements of array after delete are : 10 20 40 50
2차원 배열을 이용한 구현

#include <stdio.h>
int main(){
int numArr[3][4] = {{ 11, 22, 33, 44 }, { 55, 66, 77, 88 },
{ 99, 110, 121, 132 }};
printf("배열의 크기는 %d이다.\n", sizeof(numArr)); //정수 = 4바이트
int col = sizeof(numArr[0]) / sizeof(int); //배열의 가로 크기
int row = sizeof(numArr) / sizeof(numArr[0]); //배열의 세로 크기
printf("배열의 가로 크기는 %d이다.\n", col);
printf("배열의 세로 크기는 %d이다.\n", row);
return 0;
}
result
배열의 크기는 48이다.
배열의 가로 크기는 4이다.
배열의 세로 크기는 3이다.배열의 원소에 대한 물리적 주소 확인
#include <stdio.h>
int main(){
int i, j, sale[3][4] = {{ 11, 22, 33, 44 }, { 55, 66, 77, 88 },
{ 99, 110, 121, 132 }};
for(i=0; i<3; i++){
for(j=0; j<4; j++){
printf("address of sale[%d][%d]=%d: %u \n", i, j, numArr[i][j],
&(numArr[i][j]));
}
}
return 0;
}
result
address of sale[0][0]=11: 6487520
address of sale[0][1]=22: 6487524
address of sale[0][2]=33: 6487528
address of sale[0][3]=44: 6487532
address of sale[1][0]=55: 6487536
address of sale[1][1]=66: 6487540
address of sale[1][2]=77: 6487544
address of sale[1][3]=88: 6487548
address of sale[2][0]=99: 6487552
address of sale[2][1]=110: 6487556
address of sale[2][2]=121: 6487560
address of sale[2][3]=132: 6487564
3차원 배열을 이용한 구현
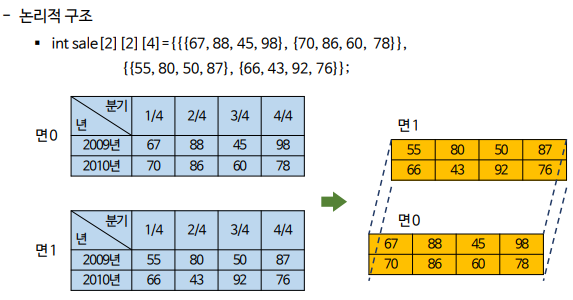

배열의 원소에 대한 물리적 주소 확인
#include <stdio.h>
int main(){
int i, j, k, sale[2][2][4]={{{67, 88, 45, 98}, {70, 86, 60, 78}},
{{55, 80, 50, 87}, {66, 43, 92, 76}}};
for(i=0; i<2; i++){
for(j=0; j<2; j++){
for(k=0; k<4; k++){
printf("address of sale[%d][%d][%d]]=%d: %u \n", i, j, k,
sale[i][j][k], &(sale[i][j][k]));
}
}
}
return 0;
}
result
address of sale[0][0][0]]=67: 6487504
address of sale[0][0][1]]=88: 6487508
address of sale[0][0][2]]=45: 6487512
address of sale[0][0][3]]=98: 6487516
address of sale[0][1][0]]=70: 6487520
address of sale[0][1][1]]=86: 6487524
address of sale[0][1][2]]=60: 6487528
address of sale[0][1][3]]=78: 6487532
address of sale[1][0][0]]=55: 6487536
address of sale[1][0][1]]=80: 6487540
address of sale[1][0][2]]=50: 6487544
address of sale[1][0][3]]=87: 6487548
address of sale[1][1][0]]=66: 6487552
address of sale[1][1][1]]=43: 6487556
address of sale[1][1][2]]=92: 6487560
address of sale[1][1][3]]=76: 6487564
학습 정리
- 리스트, 스택, 큐와 같은 순차구조와 트리, 그래프와 같은 비순차구조는 프로그램으로 구현하는 방식에 따라 순차 자료구조와 연결 자료구조로 나눌 수 있다
- 순차 자료구조는 구현할 자료들을 논리적인 순서대로 메모리에 연속하여 저장하는 구현 방식이다. 따라서 순차 자료구조는 논리적인 순서와 물리적인 순서가 항상 일치해야 한다
- 일반적으로 순차 자료구조는 배열을 통해 구현하고, 연결 자료구조의 경우 포인터 개념을 이용하여 구현할 수 있다
- 선형 리스트(순차 리스트)는 자료를 구조화하는 가장 기본적인 방법으로 자료를 나열한 목록 또는 자료들 간에 순서를 갖는 리스트이다.
- 선형 리스트의 삭제/삽입 시 원소들의 순서를 만족하기 위해 후속 원소들을 한 자리씩 전후로 이동해야 한다
- 배열은 동일한 자료형(기본 자료형, 구조체, 포인터등)들이 (색인, 원소)의 순서쌍으로 집단화한 선형 자료구조(순차적 저장, 유한 집합)이다.
반응형
'23년 이전 글 > 자료구조' 카테고리의 다른 글
| 스택 자료구조 (0) | 2022.07.26 |
|---|---|
| 재귀함수 (0) | 2022.07.25 |
| 구조체와 범용 리스트 (0) | 2022.07.24 |
| 추상 자료형, 알고리즘 (0) | 2022.07.06 |
| 자료구조 종류와 표현 방법 (0) | 2022.07.06 |
