추상화와 추상 자료형
추상화(abstraction)
크고 복잡한 자료, 모듈, 시스템 등으로부터 핵심적인 개념 또는 기능을 간추려 내어 주어진 문제를 해결하기 위한 것
- 불필요한 부분을 생략하고 객체의 속성 중 가장 중요한 것에만 중점을 두는 것
- 추상화의 예) 아날로그 시계, printtf("******..."); 100개 별을 반복문으로.
- 추상화를 통해 코드의 재 사용성, 가독성을 높이고, 생산성의 증가, 에러 감소, 유지 보수에 있어 많은 시간을 줄일 수 있음
추상화의 범주
자료 추상화 - 계산될 자료의 특성을 추상화 하는 것
프로시져(제어 혹은 알고리즘) 추상화 - 실행 순서를 제어하는 특성을 추상화 하는 것
추상화와 구체화 비교
추상화 - 무엇인지를 논리적으로 정의 -> 알고리즘 정의
구체화 - 어떻게 할 것인지 실제적으로 표현 -> 프로그램 구현
추상화의 목적
가독성, 재사용성, 유지 보수의 용이함
소프트웨어를 명세부와 구현부로 분리하는 정보 은닉을 지원
- 객체들의 구현은 외부 요구에 영향을 적게 받음
- 보안성- 구현의 세부사항을 프로그램의 다른 부분이 변경할 수 없음
자료 추상화
데이터의 물리적인 표현을 의식하지 않고 현실세계의 사물을 개념화, 단순화 한 것
- 자료형을 기술하기 위한 도구로 객체지향기법의 기본이 되는 개념
- 객체 정의 시 자료형과 기능적인(연산) 측면으로 분리 정의하여 데이터에 대한 조작을 효과적으로 수행할 수 있는 수단을 제공
- 자료 추상화의 관점에서 자료형을 정의하면 의미가 명확해지고 간결해짐
- 기본적 추상화 - 컴퓨터 내부 자료 표현을 추상화하는 것(int i;, x = 2.5;)
- 구조적 추상화 - 관련된 자료값의 집합을 추상화하는 것(typedef struct_Person)
- 단위 추상화 - 프로그램 전체 정보에 대한 추상화로서 자료의 생성, 사용에 대한 정보를 모아두는 것(class student)
프로시져 추상화
제어 또는 알고리즘 추상화로 실행 순서를 제어하는 특성을 추상화한 것
- 기본적 추상화 - 기계 명령어들을 모아 추상구문으로 바꾸는 것, 예) x:= x+y(계산과 값의 저장 추상화)
- 구조적 추상화 - 검사 값에 따른 명령어 그룹을 실행하는 것 예) switch - case, if, for, while
- 단위 추상화 - 프로시져(특정 작업을 실행)의 집합을 추상화하는 것(프로그램 들을 모아 하나의 단위프로그램으로)
자료와 프로시져 추상화
자료 : 컴퓨터 내부에서 표현하고자 하는 자료구조로서, 프로그램의 처리 대상이 되는 것
연산 : 자료에 대해 수행할 연산자(함수명칭)의 집합으로서 어떤 일을 처리하는 과정을 의미

추상 자료형
자료 추상화를 통해 정의되는 자료형으로 자료 및 연산을 모두 하나의 단위로 묶어 자료형에 속하는 값들의 집합을 고려한 후 적용 가능한 연산들을 정의해가면서 추상화시켜 구현하는 것.
새로운 자료형을 자료와 연산자의 특성을 논리적으로 추상화하여 정의한 자료형
특징
- 데이터와 연산의 본질에 대한 명세만 정의할 수 있음
- 사용자의 데이터 종류 및 사용자 각 연산 기능을 정의
- 기존의 데이터 타입을 이용하고 확장이 가능
- 캡슐화 또는 정보은닉이 가능함
- 자세한 구현 외에 표면 기능만 제공하여 사용자에게 특정한 일을 하기 위한 방법을 알려줄 수 있음.
- 메소드가 무얼 하는지 알 수 있지만, 어떻게 실행하는지 사용자는 알 수 없음
추상 자료형 예시

알고리즘의 개요
알고리즘
- 대수학자인 알고리즈미에서 유래
- 어떤 문제를 해결할 때 그 절차나 방법을 알기 쉽도록 기술하는 논리적인 절차과정을 의미
- 컴퓨터에 의해 수행 가능해야 하고, 프로그램 작성이 가능해야 함
알고리즘 연구 분야
고안
- 완벽한 자동화를 통한 알고리즘의 개발은 거의 불가능함
- 이미 증명된 유용한 알고리즘들을 통해 보다 유용한 알고리즘을 개발하는데 그 의미가 있음
고안된 알고리즘의 검증
- 입력값에 대하여 올바른 결과를 계산해 내는지를 밝히는 절차가 필요
- 프로그래밍 언어와는 독립적으로 올바르게 작동할 수 있음을 검증
분석
- 고안된 알고리즘의 실행을 위해 필요한 실행시간과 기억장치를 결정
테스트
- 디버깅, 성능분석
알고리즘의 개발
알고리즘의 목표
자료에 대해 수행할 연산(삽입, 삭제 등) 결정 -> 알고리즘 작성
단순히 원하는 결과를 얻을 수 있는 알고리즘이 아닌 처리시간이나 기억장소 사용측면에서 효율적인 알고리즘을 개발
- 자료구조에 따라 적용할 알고리즘이 다양
- 선택된 자료구조를 기반으로 수행될 연산을 단계적으로 표현
- 문제를 확실히 이해해야, 맞는 알고리즘을 개발할 수 있음
모든 문제에 대한 알고리즘 존재 여부
주어진 문제를 해결하기 위한 알고리즘을 찾을 수 없는 문제도 있음
예) 체스나 장기를 두는 문제일 경우
- 이론적으로 완벽한 알고리즘은 가능
- 말의 움직임에 대한 모든 가능성을 고려하면 실행시키는데 엄청난 시간과 기억공간이 필요
알고리즘이 갖추어야 할 조건

알고리즘 표현 방법

알고리즘의 분석
알고리즘 분석 이유 및 기준
분석이유
- 같은 문제를 해결하는데 여러 가지 알고리즘이 존재할 수 있음
- 주어진 상황에 따라서 적절한 알고리즘을 선택해야 함(최상은 없음)
- 문제 해결 속도에 비중을 둘 것인지, 알고리즘 단수성에 더 비중을 둘 것인지에 따라 알고리즘 선택이 달라짐
- 최적 알고리즘 선택은 적용 가능한 여러 알고리즘들을 서로 비교 분석함으로써 가능해짐
분석기준
컴퓨터에서의 실행시간과 기억공간
- 컴퓨터 기종 및 작성할 프로그램 언어와 작성자에 의존
- 실행시간 측정에 따른 프로그램 작성 및 수정 시간 소요
- 모든 플랫폼에서 동일한 결과를 산출하진 못함
점근적 복잡도(complexity)
알고리즘이 주어진 데이터의 크기를 기준으로 비교할 수 있는 객관적인 기준을 의미함
- 실행시간 소요량(계산량, 실행 빈도수, 차수) = 시간복잡도
- 기억장소 사용량 = 공간복잡도
시간복잡도
프로그램을 실행시켜 완료하는데 걸리는 시간
- 표현식 : Tp = Tc(컴파일시간) + Te(실행 시간 각 명령문 하나를 실행하는데 걸리는 시간)
프로그램의 시간복잡도 분석은 실행 빈도수(frequency count)를 계산함
- 기본 연산의 실행횟수 파악(명령문 개수)
- 실질적 각 명령문의 실행 시간은 다르지만 한 단계로 계산되는 모든 명령문의 실행시간 같다고 가정
- 보조연산은 작업에 독립적(초기값 설정, 반복구조의 반복횟수 등)
- 가장 기본적인 연산 부분만을 고려한 실행횟수 파악
- 알고리즘의 전체 연산 횟수는 데이터 크기에 상관없이 기본연산 횟수에 비례

계산량 표현 방법
입력 데이터 크기의 함수로 표현함
- 기본연산 횟수는 입력 데이터의 크기에 따라 다름
- 명단에서 'x'를 찾기 => 명단 내 이름의 개수
- 두개 행렬을 곱하기 => 행렬 크기
- 수치 목록을 오름차순으로 정렬 => 목록 내의 원소의 개수
- 입력 데이터의 크기가 동일한 경우 입력 데이터의 상태에 따라 다름
- 입력데이터 A = {1,2,3,4,5}
- 입력데이터 B = {5,4,3,2,1}
계산량(실행빈도수) 구하는 예 1
피보나치 값을 계산하는 프로그램

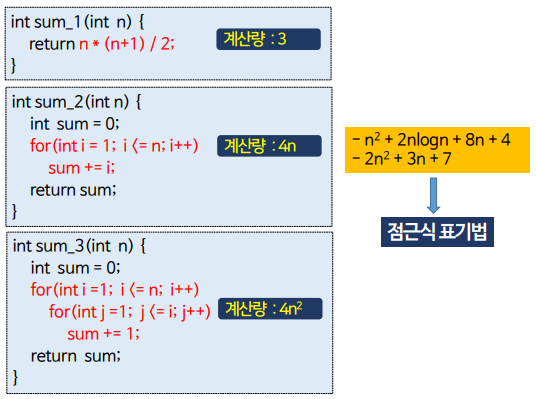
계산량(실행빈도수) 구하는 예 2
1~n까지 합을 계산하는 프로그램

공간 복잡도
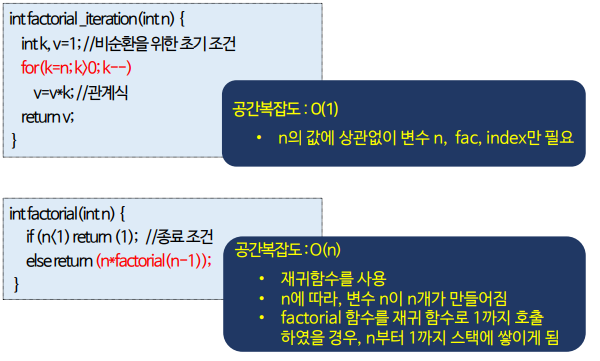
소요 기억공간 구하는 예
n! ( =1 * 2 * ... *n) 구하기
점근식 표기법(asymptotic notation)
Big-O 표기
f, g가 양의 정수를 갖는 함수, 두 양의 상수 c, n0 , 모든 n >= n0 에 대해 f(n) ≤ c.g(n)이다 => 「 f(n) = O(g(n))」
- g(n)을 f(n)의 점근 상한(asymptotic upper bound)
- 주어진 알고리즘이 아무리 나빠도 비교하는 함수와 같거나 좋음
예시


Big - θ 표기
- f, g가 양의 정수를 갖는 함수, 두 양의 상수 c1, c2, n0 모든 n >= n0에 대해 c1.g(n) <= f(n) <= c2.g(n) => f(n) = θ(g(n))
- g(n)을 f(n)의 점근 상한 및 하한 (asymptotic tight bound)
- 주어진 알고리즘이 아무리 좋아도 비교하는 함수의 범위 안에 있음

계산량 함수의 증가율

내용 정리
- 추상화는 크고 복잡한 자료, 모듈, 시스템 등으로부터 불필요한 부분을 생략하고 객체의 속성 중 가장 중요한 것에만 중점을 두어 모델화 한 것
- 자료 추상화는 자료의 물리적인 표현을 의식하지 않고 현실세계의 사물을 개념화, 단순화 한 것으로 데이터적인 측면(자료형)과 기능적인 측면(연산)으로 분리 정의하여 자료에 대한 조작을 효과적으로 수행할 수 있는 수단을 제공한다.
- 추상 자료형은 자료 및 연산을 모두 하나의 단위로 묶어 자료형에 속하는 값들의 집합을 고려한 후 적용 가능한 연산들을 정의해가면서 자료와 연산자의 특성을 논리적으로 추상화하여 정의한 자료형이다.
- 알고리즘은 어떤 문제를 해결할 때 그 절차나 방법을 알기 쉽도록 기술하는 논리적인 절차로서 프로그램 작성을 통해 컴퓨터에서 수행 가능해야 한다.
- 알고리즘을 분석하는 이유는 적용 가능한 여러 알고리즘들을 서로 비교 분석함으로써 최적의 알고리즘을 선택하는데 있다.
'23년 이전 글 > 자료구조' 카테고리의 다른 글
| 스택 자료구조 (0) | 2022.07.26 |
|---|---|
| 재귀함수 (0) | 2022.07.25 |
| 구조체와 범용 리스트 (0) | 2022.07.24 |
| 선형 리스트와 배열 (0) | 2022.07.23 |
| 자료구조 종류와 표현 방법 (0) | 2022.07.06 |
