Auto-regressive Integrated Moving Average
시계열 예측에 사용되는 다양한 모델중 하나, 페이스북의 Prophet, LSTM 딥러닝 등
시계열 데이터(Time-Series)
시간 순서대로 발생한 데이터의 수열이라는 뜻

미래 예측은 사실상 불가능하지만 특정한 전제조건 아래에선 가능
1. 과거의 데이터에 일정한 패턴이 있음
2. 과거의 패턴은 미래에도 동일하게 반복됨
즉 안정적이고, 통계적 특성이 변하지 않는 데이터에 한해 예측 가능
Stationary Series의 기준
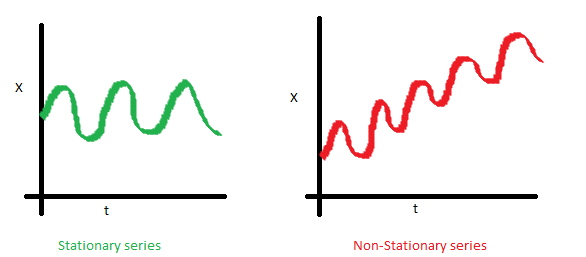

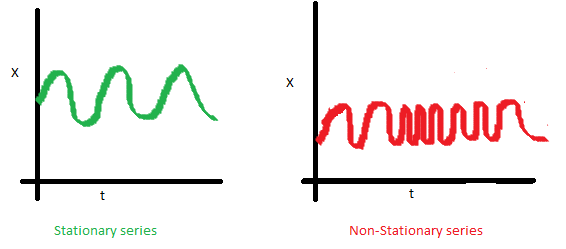
평균, 분산, 공분산
평균으로 분포의 중간을 알아내고, 분산으로 분포가 얼마나 퍼져있는지 알아내며
각 확률 변수들이 어떻게 퍼져있는지 나타내는 것은 공분산이다(Covariance)
확률변수 X의 평균(기대값), Y의 평균을 각각

X,Y의 공분산은 아래와 같다.

공분산은 X의 편차와 Y의 편차를 곱한것의 평균이라는 뜻

단, 공분산은 X,Y의 단위에 크게 영향을 받으므로 이를 보완하기 위해 상관계수(Correlation)가 도입된다
상관계수는 절대값 1을 넘을 수 없으며, X,Y가 독립이라면 상관계수는 0
선형관계라면 1 또는 -1이다

Autocovariance, Autocorrelation
여기서 Auto의 의미는 self를 의미

자신의 공분산을 구할 경우 그냥 분산이 될텐데 공분산이라고 표현하는 이유는
완전한 자신이 아닌, h값만큼 이동한 자신과의 공분산이기 때문
따라서 Xt가 자신이고 Xt+h와 공분산을 구하는 것이 Autocovariance, 이러한 함수는 Autocovariance Function
특징
1.h에 대한 자기공분산은 자체 자기공분산 보다는 작거나 같다, 이유는 자기 상관계수는 항상 -1보단 크거나 같고, +1보다는 작거나 같기 때문
2. h에 대한 자기공분산은 -h에 대한 자기공분산과 같다. 직관적으로 h만큼 떨어진 신호와의 자기공분산이나 h만큼 떨어진 데이터의 입장에선 -h와의 자기 공분산이므로 이는 같을 수 밖에 없다
예시
직전 5년 치 판매량 X(t-4), X(t-3), X(t-2), X(t-1), X(t)를 가지고 X(t+1) 예측하기에는
t에 무관하게 예측이 맞아 떨어져야 함
t에 무관하게 평균과 분산이 일정범위 안에 있어야하고 t에 무관하게 h에 대해서만 달라지는 일정한 상관도가 필요
이때에는 예측이 가능
Augmented Dickey-Fuller Test
시계열 데이터의 Stationary 여부를 체크하는 통계적인 방법
1. 시계열 데이터가 안정적이지 않다는 귀무가설(Null Hypothesis)
2. 통계적 가설 검정 과정을 통해 이 귀무가설이 기각될 경우
3. 이 시계열 데이터가 안정적이라는 대립가설(Alternative Hypothesis)를 채택
귀무가설, 대립가설, p-value
통계에서의 가설은 어떤 모집단의 모수(평균,분산등)에 대한 잠정적인 주장
귀무가설은 처음부터 버릴 것을 예상하는 가설로 차이가 없거나 의미있는 차이가 없는 경우의 가설로서 이것이 맞거나 맞지 않다는 통계학적 증거를 통해 증명하려는 가설
예) 전국 남학생 평균키가 170cm라는 주장을 통계적으로 검정한다면
귀무가설은 전국 남학생의 평균키는 170과 같다, 또는 차이가 없다
~와 차이가 없다, ~의 효과가 없다등의 형식으로 설정
대립가설은 귀무가설이 거짓이라면 대안으로 참이 되는 가설로, 전국 남학생의 평균키가 170cm이라는 통계적으로 검정시 전국 남학생의 평균 키는 170cm와 다르다, 또는 차이가 있다로 표현이 가능
p-value의 정의는 귀무가설이 참이라고 가정했을 때 표본으로 얻어지는 통계치(표본평균 등)가 나타날 확률로
p값이 낮다는 것은 귀무가설이 참이라는 가정하에 표본을 추출했을 때 이런 통계량이 관측될 확률이 낮다는 의미
P값이 낮으면 표본 통계량이 우연히 나타나기 어려운 케이스이기 때문에 귀무가설을 기각하고 대립가설을 채택
ADF 검정
1979년 David Dickey와 Wayne Fuller에 의해 개발된 DF 검정을 일반화한 것
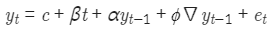
에서 ADF 검정은 DF 검정에 P lag의 차분을 추가해 검정능력 강화
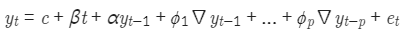
검정 통계량이 Critical value보다 작거나 p-value가 설정한 유의수준 값보다 작으면 정상적인 시계열 데이터
Augmented Dickey-Fuller (ADF) Test - Must Read Guide - ML+
Augmented Dickey Fuller test (ADF Test) is a common statistical test used to test whether a given Time series is stationary or not. It is one of the most commonly used statistical test when it comes to analyzing the stationary of a series
www.machinelearningplus.com
정상성을 알아보기 위한 단위근 검정 방법
단위근(unit root)는 x = 1, y = 1인 해로 시계열 자료에서 예측할 수 없는 결과를 가져올 수 있음
자료에 단위근이 존재한다는 귀무가설

단위근이 존재하지 않아 시계열 자료가 정상성을 만족한다는 대립가설

이렇게 2가지 가설을 세우고 검정을 통해 귀무가설을 기각하면 정상성을 띰
ARIMA(Autoregressive Integrated Moving Average)
시계열 데이터는 Trend, Seasonality, Residual로 나눌 수 있으며 Trend, Seasonality로 분리할 경우 Residual이 예측력 있는 안정적인 시계열 데이터가 됨
ARIMA를 사용하면 이 원리를 이용해 시계열 데이터의 예측 모델을 자동으로 만들기 가능
AR(자기회귀, Autoregressive)

과거 값들에 대한 회귀로 미래 값을 예측

AR은 시계열의 Residual에 해당하는 부분을 모델링
가중치 크기가 1보다 작은 Y의 가중합으로 수렴하는 자기회귀 모델과 안정적 시계열은 통계학적으로 동치
주식값이 일정한 균형 수준을 유지할 것이라고 예측하는 관점이 주식 시계열을 AR로 모델링하는 관점
MA(이동평균, Moving Average)

MA는 Yt가 이전 q개의 예측 오차값의 가중합으로 수렴한다고 보는 모델
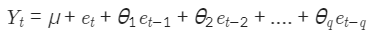
MA는 시계열의 Trend 부분을 모델링
예측 오차값 e t-1이 0보다 크면 모델 예측보다 관측값이 높으므로 다음 Y예측시 예측치를 올려잡음
주식값이 최근 증감 패턴을 지속할 것이라고 보는 관점이 MA 모델링의 관점
I(차분 누적, Integration)
I는 Yt 이전 데이터와 d차 차분의 누적합이라고 보는 모델
I는 시계열의 Seasonality에 해당하는 부분을 모델링
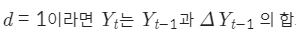
ARIMA 모델의 모수

p 와 q는 일반적으로 p + q < 2, p * q = 0의 값을 사용, 이는 많은 시계열 데이터가 AR 또는 MR중 하나의 경향을 띄기 때문
ACF(Autocorrelation Function)
- 시차에 따른 관측치들 사이에 관련성 측정 함수
- 주어진 시계열의 값이 과거 값과 어떻게 상관되는지 설명
- ACF plot에서 X축은 상관 계수를, y축은 시차수를 나타냄
PACF(Partial Autocorrelation Function)
- 다른 관측치 영향력 배제하고 시차 관측치간 관련성 측정
- k 이외 모든 시차를 갖는 관측치의 영향력을 배제하고 특정 두 관측치 Yt, Yt-k가 얼마나 관련있는지 나타내는척도
A Gentle Introduction to Autocorrelation and Partial Autocorrelation
Autocorrelation and partial autocorrelation plots are heavily used in time series analysis and forecasting. These are plots that graphically summarize […]
machinelearningmastery.com
실습예제는 깃허브로 대체합니다
GitHub - dlfrnaos19/rock_scissors_paper_classifier: task 1
task 1. Contribute to dlfrnaos19/rock_scissors_paper_classifier development by creating an account on GitHub.
github.com
'23년 이전 글 > 모두의연구소 아이펠' 카테고리의 다른 글
| -32일차- 활성화함수 (0) | 2022.02.14 |
|---|---|
| -31일차- 정규화와 정칙화 (0) | 2022.02.11 |
| -29일차- 딥러닝 레이어 이해하기 2 (0) | 2022.02.09 |
| -27일차- 딥러닝 레이어의 이해 (0) | 2022.02.07 |
| -26일차- Deep Network (0) | 2022.02.04 |
