데이터를 표현하는 통계적 방법
위치(location) 척도
- 데이터의 대표값: 산술평균, 가중평균, 중앙값, 최빈값 등
산포(dispersion) 척도
- 데이터가 퍼져있는 정도
- 범위, 평균절대편차, 분산, 표준편차, 변동계수
비대칭도(Skewness)
- 자료집단이 대표치를 중심으로 좌/우 어느쪽으로 치우쳐 있는지, 치우쳤다면 얼마나 치우쳐 있는지 보여줌
- 피어슨 비대칭계수 (Pearson`s CS)
첨도(Kurtosis)
- 분포의 뾰족한 정도 측정
- 첨도계수(Coefficient of kurtosis, CK)
위치척도
데이터 집합의 중심 경향을 기술하는데 사용되는 값
위치척도 종류
- 평균
- 중위수
- 최빈값
산술 평균은 가장 널리 사용되는 위치척도임
산술평균_모평균
μ는 모평균을 의미하며 그리스어 소문자 "뮤"를 활용하여 표현함
N은 모집단 내의 값의 개수
x는 어떤 특정한 값
Σ는 그리스어 대문자 "시그마"이며 더하기 연산을 의미
Σx는 모집단 x값의 총합을 의미함
모집단의 측정 가능한 특성은 모수(parameter)라 하며, 모평균은 모수의 대표적인 예시임
산술평균_표본평균
x̄는 표본평균을 의미하며 "엑스바"로 읽음
n은 표본의 개수
x는 어떤 특정한 값
측정 가능한 표본의 특성을 표본통계량(Sample statistics)라 하며 표본평균은 표본 통계량의 대표적인 예시임
산술평균의 특성
- 등간척도 또는 비율척도가 요구됨
- 평균 계산에 모든 데이터 값들이 포함되어야 함
- 평균은 유일한 값
- 평균으로부터 각 값들까지의 편차의 합은 0
중위수(median)
최소에서 최대의 순서로 정렬된 값들의 중간점
중위수 위, 아래 각각 50%의 데이터가 존재하며 전체 데이터 수가 짝수일 경우 중앙 두 값의 산술평균이 중위수
중위수의 특성
- 적어도 순서척도가 요구됨
- 중위수보다 큰 관측치는 전체의 50%, 작은 관측치도 전체의 50%
- 중위수는 데이터 집합 안에 단 하나만 존재
| 주문가격(오름차순) | 주문가격(내림차순) | |
| 60000 | 275000 | |
| 65000 | 80000 | |
| 70000 | 중위수 | 70000 |
| 80000 | 65000 | |
| 275000 | 60000 |
예)
10명의 표본으로 이루어진 성인의 지난 달 페이스북 사용 시간
3, 5, 7, 5, 9, 1, 3, 9, 17, 10 (정렬전)
1, 3, 3, 5, 5, 7, 9, 9, 10, 17 (정렬후)
(5+7) / 2 중위수는 6
최빈값
가장 빈번하게 출현하는 관측치 값
최빈값의 특성
- 명목척도 데이터에서도 사용될 수 있음
- 극도로 작거나 큰 값에 영향 받지 않음
- 평균, 중앙값과 달리 값이 여러개일 수 있음 -> 이봉분포(Bimodal distribution) : 최빈값이 2개일 경우
- 데이터에 따라 존재하지 않을 수도 있음
평균, 중위수, 최빈값의 상대적 위치
평균, 중위수, 최빈값 및 왜도
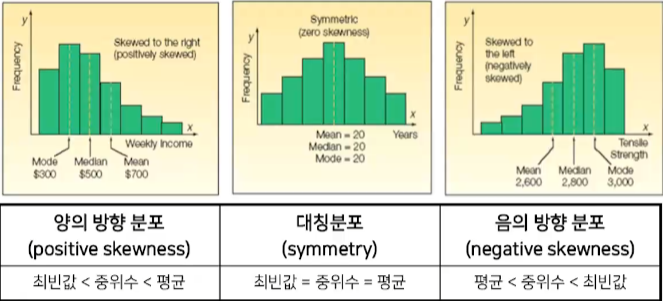
- 분포의 양, 음은 꼬리의 방향에 의해 좌우됨
- 최빈값은 항상 분포의 봉우리에 나타남
- 기울어진 분포의 경우 평균은 분포의 꼬리 방향에 나타남
- 중위수는 언제나 최빈값과 평균의 사이에 나타남
반응형
'23년 이전 글 > 통계' 카테고리의 다른 글
| 데이터의 표현 (0) | 2022.06.13 |
|---|---|
| 데이터의 위치 (0) | 2022.06.13 |
| 통계 변수 (0) | 2022.06.06 |
| 통계학이란? (0) | 2022.06.06 |
| 가설검정 (0) | 2022.06.06 |
