집중화 경향 대표값, 평균
평균(mean, 산술평균)으로 주어진 수의 합을 수의 개수로 나눈 값
모집단의 평균 : μ, 표본의 평균 : x̄
단점 : 이상치가 있을 시 영향을 크게 받음
중앙값
어떤 주어진 값들을 크기의 순서대로 정렬했을 때, 가장 중앙에 위치하는 값, 이상치 영향을 피할 수 있음
ex) 값이 홀수인 경우 : 1, 2, 100 중앙값은 2
ex) 값이 짝수인 경우 : 1, 2, 90, 100 (2 + 90) / 2 = 46, 중앙값은 46
최빈값
가장 많이 관측되는 수, 즉 주어진 값 중에서 가장 자주 나오는 값
ex) [1, 3, 6, 6, 6, 7, 7, 12, 12, 17]의 최빈값은 6
연속형 변수 일 경우? 50<= ? < 60 등으로 구간을 나누고 구간 빈도가 높은 곳을 최빈값으로 선정
분산도
데이터가 흩어져 있는 정도
범위
단순히 최대값과 최소값의 차를 나타내는 값으로 간단히 구할 수 있지만 분포의 양상은 설명하지 못함
평균편차(mean deviation) 또는 절대편차(absolute deviation)
평균과 개별 관측값 사이 거리의 평균으로 각 측정치에서 전체 평균을 뺀 절대값으로 표시되는 편차의 평균

분산
각 관측값에서 전체 평균을 뺀 값의 제곱의 평균을 말함
- 평균편차가 유용하긴 하나 분산이 분포의 양상을 더 잘 설명함
- 모집단의 분산 : σ^2
- 표본의 분산 : S^2
예제
| C사 신약 복용 후 체중 변화 | L사 신약 복용 후 체중 변화 |
| +2kg | +4kg |
| +2kg | 0 |
| -2kg | 0 |
| -2kg | -4kg |
| 평균: 0kg 평균편차: 2kg 분산: 5.33 |
평균: 0kg 평균편차: 2kg 분산: 10.67 |
평균이 μ(모집단 평균)일 때 모집단의 분산

표준편차
편차를 제곱하면 단위가 없어지는 분산의 단점을 해결하기 위해 분산에 제곱근을 하여 원래 단위로 돌리기 위한 값
- 모집단의 표준편차 : σ
- 표본의 표준편차 : S
# 모집단의 표준편차를 구하는 공식
from sympy import *
mu = symbols('mu') # μ
i = symbols('i') # i
n = symbols('n') # n
Xi = Indexed(X,i) # Xi
expr = sqrt((Sum((Xi - mu)**2, (i,1,n))) / n)
# 표본의 표준편차(S)를 구하는 공식
from sympy import *
S = symbols('S') # S
Xbar = symbols('Xbar') # Xˉ
n = symbols('n') # n
Xi = Indexed('X',i) # Xi
sqrt((Sum((Xi-Xbar)**2,(i,0,n)) / n))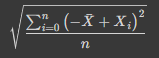
반응형
