머신러닝
머신러닝의 목표
모델이 표현하는 확률 분포를 데이터의 실제 분포에 가깝게 만드는 최적의 파라미터 값을 찾는 것
확률 변수로서의 모델 파라미터

R제곱 공간 안의 모든 점들은 일차함수들로 이루어진 함수 공간의 서로 다른 원소들에 대응됨
2차원 평면 위의 모든 점(a, b)이 하나의 일차함수 f에 대응
a,b가 위치하는 R제곱 공간을 파라미터 공간이라고 할 경우

두점 a, b를 뽑아 y=ax + b 그래프 그려보기
import numpy as np
import matplotlib.pyplot as plt
parameter_points = []
fig1, axes1 = plt.subplots(2, 5, figsize=(10, 4))
for ax in axes1.flatten():
# np.random.uniform: 정해진 구간에서 수를 무작위로 추출하여 반환합니다.
a, b = np.random.uniform(-10, 10, size=2)
a = round(a, 3)
b = round(b, 3)
parameter_points.append((a, b))
x = np.linspace(-10, 10, 50)
y = a*x + b
ax.plot(x, y)
ax.set_title('y='+str(a)+'x'+'{0:+.03f}'.format(b))
ax.set_xlim(-10, 10)
ax.set_ylim(-10, 10)
plt.tight_layout()
px, py = np.split(np.array(parameter_points), 2, axis=1)
fig2 = plt.figure()
axes2 = plt.gca()
axes2.set_title('samples from parameter space')
axes2.set_xlim(-10, 10)
axes2.set_ylim(-10, 10)
plt.scatter(px, py)
plt.show()
일차함수 모델의 파라미터 a, b를 파라미터 공간 R제곱의 원소 a, b로 본다면

평균이(1, 0)이고 표준편차가 0.5인 정규분포의 10개 점을 무작위로 뽑고, 대응되는 일차함수의 그래프를 그려보면
parameter_points = []
fig, axes1 = plt.subplots(2, 5, figsize=(10, 4))
for ax in axes1.flatten():
# np.random.normal: 정규분포를 따르는 확률 변수의 랜덤한 값을 반환합니다.
a, b = np.random.normal(loc=[1, 0], scale=0.5)
a = round(a, 3)
b = round(b, 3)
parameter_points.append((a, b))
x = np.linspace(-10, 10, 50)
y = a*x + b
ax.plot(x, y)
ax.set_title('y='+str(a)+'x'+'{0:+.03f}'.format(b))
ax.set_xlim(-10, 10)
ax.set_ylim(-10, 10)
plt.tight_layout()
px, py = np.split(np.array(parameter_points), 2, axis=1)
fig2 = plt.figure()
axes2 = plt.gca()
axes2.set_title('samples from parameter space')
axes2.set_xlim(-10, 10)
axes2.set_ylim(-10, 10)
plt.scatter(px, py)
plt.show()

posterior, prior, likelihood
posterior : 사후확률
prior : 사전확률
likelihood: 우도, 가능도
데이터의 집합 X가 주어졌을 때 데이터를 따르는 확률 분포p(X)가 존재할 것이고
머신러닝을 통해 p(X)를 가장 잘 나타내는 일차함수 모델 y=ax+b=θ⊤x를 찾는 것

데이터를 관찰하기 전 파라미터 공간에 주어진 확률 분포
위의 코드에선 평균이(1,0), 표준편차가 0.5인 정규분포prior는 일반적인 정규분포 또는 데이터 특성이 반영된 특정 확률 분포가 될 수도 있음
만약 prior 분포를 고정시킨다면 주어진 파라미터 분포에 대해서 우리가 갖고 있는 데이터가
얼마나 그럴듯한지 계산할 수 있으며, 이것이 likelihood(가능도,우도)

likelihood가 θ에 의해 결정되는 함수라는 것을 강조하기 위해 가능도 함수를 L(θ∣x)로 표기하기도 함
likelihood가 높으면 지정한 파라미터 조건내에 데이터가 관찰될 확률이 높으며, 데이터 분포를 모델이 잘 표현하는 것
데이터를 likelihood 값이 최대화 하는 방향으로 학습시키는 방법이 최대 가능도 추정(maximum likelihood estimation,MLE)
반대로 데이터 집합 X가 주어졌을 때 파라미터 θ의 분포 p(θ∣X)를 생각할 경우
데이터를 관찰한 후 계산되는 확률에서 posterior(사후 확률)이라고 함데이터의 개수는 유한하기 때문에 데이터가 따르는 확률 분포 p(X)는 정확하게 알 수 없으므로
파라미터 를 조절해가며 간접적으로 근사하는 것
머신러닝은 posterior를 직접 계산해서 최적의 θ값을 찾는 것이 아니라, prior와 likelihood의 관한 식으로 변형한 다음 그 식을 최대화하는 파라미터를 찾는 것.
이렇게 posterior를 최대화 하는 방향으로 모델 학습을 하는 방법이 최대 사후 확률 추정(maximun a posteriori estimation, MAP)이라고 함
확률 곱셈 정리에 의해 확률 변수 X와 θ의 joint probability p(X,θ)는p(X, θ) = p(θ|X)p(X) = p(X|θ)p(θ)
로 나타낼 수 있으며, 양변을 p(X)로 나누어주면 베이즈 정리와 같은 식이 나옴

likelihood와 머신러닝

머신러닝에서의 지도학습은
데이터 x와 라벨 y가 짝 지어진 형태이며 모델이 선형 모델 y=θ⊤x 로 표현할 때 예측 값은 θ⊤xn이며 이 값과 라벨 yn의 차이는 노이즈가 됨

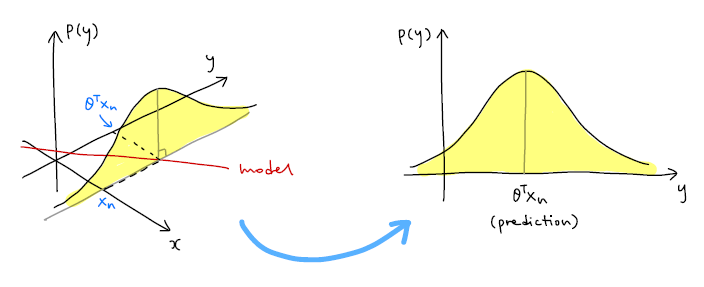
xy 평면위에 모델에 해당하는 빨간 직석이 있으며 출력값의 분포를 나타내기 위해 p(y)좌표축을 추가
입력데이터가 xn일 때 모델의 예측값은 θ⊤xn 이고 출력값의 분포 p(yn∣θ,xn)는 노란색으로 표시한 정규분포 그래프와 동일
likelihood 코드 예제
import math
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(321)
input_data = np.linspace(-2, 2, 5)
label = input_data + 1 + np.random.normal(0, 1, size=5)
plt.scatter(input_data, label)
plt.show()
# model: y = ax + b
# a, b 값을 바꾸면서 실행해보세요
#-------------------------------#
a = 1
b = 1
#-------------------------------#
# 모델 예측값
model_output = a*input_data + b
likelihood = []
# x: 입력데이터, y: 데이터라벨
# 예측값과 라벨의 차이를 제곱해 exp에 사용
for x, y, output in zip(input_data, label, model_output):
likelihood.append(1/(math.sqrt(2*math.pi*0.1*0.1))*math.exp(-pow(y-output,2)/(2*0.1*0.1)))
model_x = np.linspace(-2, 2, 50)
model_y = a*model_x + b
fig, ax = plt.subplots()
ax.scatter(input_data, label)
ax.plot(model_x, model_y)
for i, text in enumerate(likelihood):
ax.annotate('%.3e'%text, (input_data[i], label[i]))
plt.show()
데이터가 모델 함수에서 멀어질수록 데이터의 likelihood는 기하급수적으로 감소
MLE : 최대 가능도 추론
데이터셋 전체에 대한 likelihood

좋은 머신러닝 모델은 모든 데이터에 대한 likelihood값을 크게 만드는 모델
데이터가 서로 독립이고, 같은 확률 분포일때

MLE를 실제 적용할때는 log likelihood를 최대화하는 파라미터를 구하며, 로그를 씌우는 이유는 곱셈 연산이
덧셈연산으로 바뀌면서 미분 계산이 편리해지기 때문
또한 로그 함수는 단조 증가(monotonically increasing)하므로 likelihood를 최대화하는 파라미터와 log likelihood를 최대화하는 파라미터 값이 동일하여 학습 결과도 동일함, 또한 계산 범위를 한정하여 언더플로우 예방효과도 있음

θ와 관계 없는 부분을 빼고 식을 정리하면

최소제곱법의 식과 동일함
최소제곱법은 선형 모델에서 노이즈 분포가

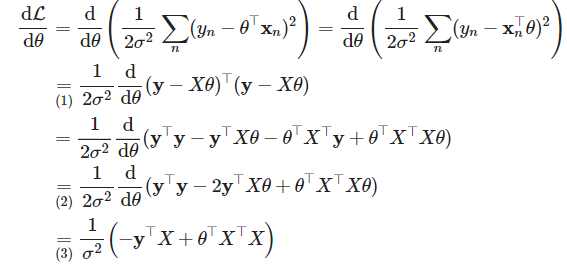


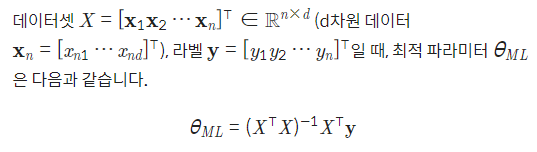
예제 데이터셋
import math
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
num_samples = 20
input_data = np.linspace(-2, 2, num_samples)
labels = input_data + 1 + np.random.normal(0, 0.5, size=num_samples)
plt.scatter(input_data, labels)
plt.show()
데이터의 likelihood와 negative log likelihood의 계산식

데이터 묶음 X의 크기

MLE 최적 파라미터 θML

def likelihood(labels, preds):
result = 1/(np.sqrt(2*math.pi*0.1*0.1))*np.exp(-np.power(labels-preds,2)/(2*0.1*0.1))
return np.prod(result)
def neg_log_likelihood(labels, preds):
const_term = len(labels)*math.log(1/math.sqrt(2*math.pi*0.1*0.1))
return (-1)*(const_term + 1/(2*0.1*0.1)*np.sum(-np.power(labels-preds,2)))
# X: 20x2 matrix, y: 20x1 matrix
# input_data 리스트를 column vector로 바꾼 다음 np.append 함수로 상수항을 추가합니다.
X = np.append(input_data.reshape((-1, 1)), np.ones((num_samples, 1)), axis=1)
y = labels
theta_1, theta_0 = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), y)
print('slope: '+'%.4f'%theta_1+' bias: '+'%.4f'%theta_0)
predictions = theta_1 * input_data + theta_0
print('likelihood: '+'%.4e'%likelihood(labels, predictions))
print('negative log likelihood: '+'%.4e'%neg_log_likelihood(labels, predictions))
model_x = np.linspace(-2, 2, 50)
model_y = theta_1 * model_x + theta_0
plt.scatter(input_data, labels)
plt.plot(model_x, model_y)
plt.show()
#result
slope: 0.8578 bias: 1.2847
likelihood: 2.9724e-54
negative log likelihood: 1.2325e+02
최대 사후 확률 추정(MAP)
MLE의 최적해는 오로지 관측된 데이터 값에만 의존하므로 계산은 비교적 간단하지만
관측된 데이터에 노이즈가 많이 섞여 있는 경우, 이상치 데이터가 존재하는 경우에 안정성이 떨어질 수 있음
likelihood을 최대화하는 MLE외에 또다른 방법 최대 사후 확률 추정(maximun a posteriori estimation, MAP)
MAP은 데이터셋이 주어졌을 때 파라미터의 분포,
지도 학습일 때 posterior는 p(θ∣X,Y)
prior 분포 p(θ)는 관찰된 데이터가 없을 때 파라미터 공간에 주어진 분포이며 를 평균이 (0,0)이고 공분산 인 정규분포로 정의할 경우

MLE에서 negative log likelihood를 최소화했던 것 처럼 MAP에서도 negative log posterior를 최소화하는 파라미터 값을 구함


MLE에서

위 식의 값 0T가 되어야 하므로

MAP 최적 파라미터는

MAP as L2 regularization
P(θ)

negative log prior가 최소화되는 부분이 의 항

최소 제곱법의 정규화항과 같은 형태로 최소제곱법에선 손실함수에 파라미터의 크기에 관한 식을 더해줌으로써 파라미터가 큰 값으로 튀는 것을 막고 오버피팅을 예방했다면 조건의 MAP에서는 파라미터 분포를 평균이 (0,0)인 정규분포로 놓아서 파라미터들이 각각 0에 가까운 값으로 학습되도록 제약 조건을 걸어줌
파라미터 분포를 다른 확률 분포로 정한다면 L2 정규화와 식이 달라질 수 있지만 파라미터 값에 특정 제약 조건을 주는 점에서 효과는 동일
MLE와 MAP의 비교
데이터는 10개, 이상치 데이터 2개가 있는 형태
import math
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
num_samples = 10
input_data = np.linspace(-2, 2, num_samples)
labels = input_data + 1 + np.random.normal(0, 0.5, size=num_samples)
input_data = np.append(input_data, [0.5, 1.5])
labels = np.append(labels, [9.0, 10.0])
plt.scatter(input_data, labels)
plt.show()
MLE와 MAP의 최적 파라미터
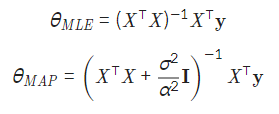
노이즈 분포 표준편차 는 0.1, 파라미터 분포 표준편차 는 0.04로 지정
정규화 상수 α제곱에 반비례 하는 값
def likelihood(labels, preds):
result = 1/(np.sqrt(2*math.pi*0.1*0.1))*np.exp(-np.power(labels-preds,2)/(2*0.1*0.1))
return np.prod(result)
def neg_log_likelihood(labels, preds):
const_term = len(labels)*math.log(1/math.sqrt(2*math.pi*0.1*0.1))
return (-1)*(const_term + 1/(2*0.1*0.1)*np.sum(-np.power(labels-preds,2)))# X: 21x2 matrix, y: 21x1 matrix
# input_data 리스트를 column vector로 바꾼 다음 np.append 함수로 상수항을 추가합니다.
X = np.append(input_data.reshape((-1, 1)), np.ones((num_samples+2, 1)), axis=1)
y = labels
# MLE 파라미터 계산식
mle_theta_1, mle_theta_0 = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), y)
# MAP 파라미터 계산식
map_theta_1, map_theta_0 = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)+(0.1*0.1)/(0.04*0.04)*np.eye(2)), X.T), y)
print('[MLE result] (blue)')
print('slope: '+'%.4f'%mle_theta_1+' bias: '+'%.4f'%mle_theta_0)
mle_preds = mle_theta_1 * input_data + mle_theta_0
print('likelihood: '+'%.4e'%likelihood(labels, mle_preds))
print('negative log likelihood: '+'%.4e\n'%neg_log_likelihood(labels, mle_preds))
print('[MAP result] (orange)')
print('slope: '+'%.4f'%map_theta_1+' bias: '+'%.4f'%map_theta_0)
map_preds = map_theta_1 * input_data + map_theta_0
print('likelihood: '+'%.4e'%likelihood(labels, map_preds))
print('negative log likelihood: '+'%.4e'%neg_log_likelihood(labels, map_preds))
model_x = np.linspace(-2, 2, 50)
mle_model_y = mle_theta_1 * model_x + mle_theta_0
map_model_y = map_theta_1 * model_x + map_theta_0
plt.scatter(input_data, labels)
plt.plot(model_x, mle_model_y)
plt.plot(model_x, map_model_y)
plt.show()
#result
[MLE result] (blue)
slope: 1.4748 bias: 2.4784
likelihood: 0.0000e+00
negative log likelihood: 4.1298e+03
[MAP result] (orange)
slope: 1.1719 bias: 1.6628
likelihood: 0.0000e+00
negative log likelihood: 4.6645e+03
파란색 직선은 MLE, 주황색 직선은 MAP
파란색 직선은 이상치 데이터를 포함한 negative log likelihood를 감소시키기 위해 직선이 위로 치우친 반면
주황 직선은 이상치 데이터가 추가되어도 아래쪽 데이터에서 크게 벗어나지 않음
'23년 이전 글 > 모두의연구소 아이펠' 카테고리의 다른 글
| -37일차- 추천시스템 (0) | 2022.02.21 |
|---|---|
| -35일차- QnA 봇 만들기 (0) | 2022.02.17 |
| -33일차- 트랜스포머로 대화형 챗봇 만들기 (0) | 2022.02.15 |
| -32일차- 활성화함수 (0) | 2022.02.14 |
| -31일차- 정규화와 정칙화 (0) | 2022.02.11 |
